Таблица котангенсов Брадиса – тесно связана с таблицей тангенсов. Это естественно, так как приставка “ко” прямо указывает нам на то, что он является обратным значением от тангенса. Это выражается и в тригонометрической формуле нахождения котангенса:
![]()
Котангенсы и тригонометрические функции, знакомство
В геометрии важную роль играют тригонометрические функции, которые объясняют, как относятся между собой углы и стороны треугольника с прямым углом. Наука не стоит на месте и развивается, так же как и тригонометрия. Есть новые решения дифференцированных уравнений, которые выражают тригонометрические функции и о которых Евклид не мог знать.
В основном, используются для вычислений значений тригонометрических функций, причем только первые из двух могут определяться только с помощью геометрии.
Синус (sin): ![]()
Косинус (cos): ![]()
Котангенс (ctg): ![]()
Тангенс (tg): ![]()
Секанс (sec): ![]()
Косеканс (cosec): ![]() .
.
Рассматривая прямоугольный треугольник, нужно учесть, что все справочные материалы дают одинаковое обозначение всех его параметров, таких как углы и стороны.
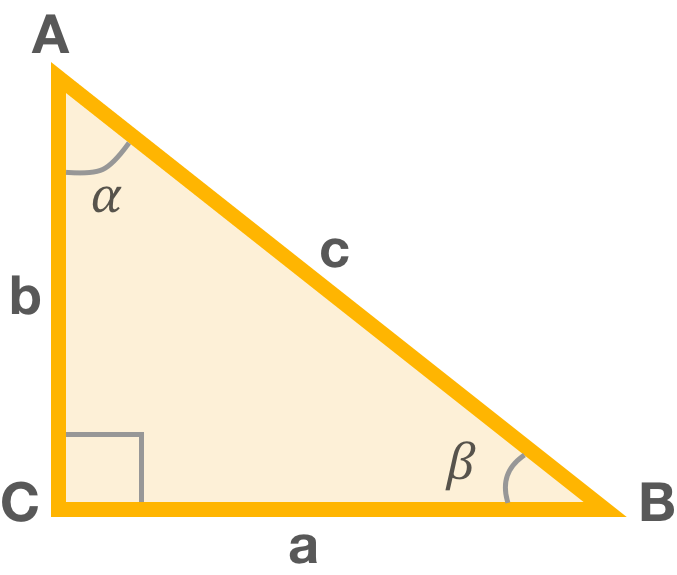
Три угла в нем обозначаются α, β, γ, причем угол 90° всегда обозначается γ. Сторона, лежащая напротив прямого угла, называется гипотенуза и обозначается всегда с. Альфа это первая буква греческого алфавита и угол, с которого начинаются все расчёты, также называется α. Сторона, или катет, лежащая напротив этого угла, называется противолежащей и называется а или ВС от названия вершин. Сторона, которая лежит рядом с углом или катет, называется прилежащей и обозначается b или АС.
По теории Евклида, который довел её раз и навсегда, сумма всех углов этого треугольника, который лежит в одной плоскости, равна 180°или числу π. И значения каждого угла будут находиться в промежутке между 0 и π /2.
Тогда тригонометрические функции можно выразить через размеры сторон этого треугольника. Так как угол α является первым и в греческом алфавите и в нашем треугольнике, начинаем знакомство с функциями через этот угол.
Синус α можно выразить через отношение катета, который противолежит углу α к гипотенузе нашего треугольника, то есть через формулу sin α = а: с.
Косинус α выражаем, соответственно, выражается через отношение катета, который лежит напротив этого угла, к гипотенузе нашего треугольника, то есть через формулу sin α = а: с. Также нужно помнить, что sin β = α: с, что позволяет принять то, что sin α равен cos β и следовательно sin β равен cos α, что помогает при решении задач.
Тангенс α равен частному от отношения противолежащего катета а к катету прилежащему b: tg α = а : b.
Соответственно, котангенс мы выражаем аналогичным способом ctg α = b : а.
Секанс угла α составляет отношение гипотенузы треугольника к катету, прилежащему к этому углу sec α = c : b, а косеканс по угла α той же теории как отношение гипотенузы треугольника к катету, который противостоит углу, cosec α = с : a.
Если задать систему координат с центром в точке О, а точка А, которая будет двигаться по окружности, образует радиус ОА. Это наглядно видно на чертеже.
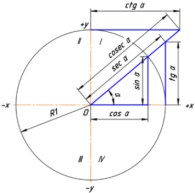
Угол поворота можно считать произвольным и, согласно принятым обозначениям, называется θ. Через эту окружность можно выражать вышеназванные функции.
Например, тангенсом этого угла θсчитается отношение ординаты точки А на окружности к её абсциссе. Тогда если ctg α = b : а, а АС = sin θ, ОС = cos θ, то tgθ = sin θ : cos θ. Аналогично получаем ctg θ = cos θ : sin θ или 1 : tgθ.
Калькулятор расчета котангенса угла
Применение функции котангенса для решения задач по тригонометрии
Для понимания того, как пользоваться тригонометрическими функциями, нужно практически решить задачу с применением этих функций.
Пример: прямоугольный треугольник АВС, катет ВС = а = 8 см, катет АС = b = 13 см. Нужно найти все недостающие размеры в треугольнике.
Первая формула, которую мы применяем, это ctg α = b : а. Тогда ctg α = 13 : 8=1, 625. Затем по таблице Брадиса для функций тангенсов и котангенсов ищем наше значение котангенса. Котангенсы углов смотрим, начиная с правой стороны таблицы. Находим значение 1,6255, которое равно 30 ° 30′, но оно больше нашего на 0,0005. Можем принять его таким, а можем отнять от найденного значения поправку в 1′. Тогда угол α = 30 ° 29′. Угол β, согласно Эвклиду, будет равен: β = 90° – 30 ° 29′ = 59° 21′.
Затем ищем гипотенузу с. Гипотенузу лучше искать через функцию синуса, то есть через sin α, который равен а: с, тогда с = а : sin α.
Обращаемся к таблице Брадиса, но уже не к значению тангенсов и котангенсов, а там, где указаны значения синуса и косинуса угла.
Ближайшее значение 30° 36′, будет 0,5060, тогда не хватает 3′, Что по полям поправок равно 0,0008. Добавляем это число к найденному: 0, 5060 + 0,0008 = 0,5068. Подставляем это значение в формулу, с = 8 : 0,5068, с = 15,8 см. Задачу мы успешно решили.
Можно искать значение углов через значение числа π, которое равно 180°. Тогда наиболее популярные углы, такие, как котангенс 30 градусов, котангенс 0 градусов, котангенс 60 градусов, котангенс 90 градусов, котангенс 45 градусов, котангенс 15 градусов, котангенс 75 градусов можно рассматривать намного проще. Нужно знать, что котангенс 0 градусов не существует, а котангенс 90 градусов равен 0.
Можно найти котангенс угла 5 градусов, который равен 11,83 и находится в таблице Брадиса котангенсов для малых углов и добавлять или отнимать от наиболее часто встречающихся углов. Например, угол 45 градусов, его котангенс равен 1, тогда котангенс угла 50 градусов будет равен 1+11,83 = 12,83. Котангенс 35 градусов можно рассчитать путем добавления к котангенсу 30 градусов угол 5 градусов.
Для удобства есть рассчитанная таблица основных углов через значение π, которое уже рассчитано. Ниже показана таблица котангенсов и тангенсов основных углов.
| Значение угла α (градусов) | Значение угла α в радианах | ctg (Котангенс) |
|---|---|---|
| Котангенс 0 | 0 | - |
| Котангенс 15 | π/12 | 3.7321 |
| Котангенс 30 | π/6 | 1.7321 |
| Котангенс 45 | π/4 | 1 |
| Котангенс 50 | 5π/18 | 0.8391 |
| Котангенс 60 | π/3 | 0.5774 |
| Котангенс 65 | 13π/36 | 0.4663 |
| Котангенс 70 | 7π/18 | 0.364 |
| Котангенс 75 | 5π/12 | 0.2679 |
| Котангенс 90 | π/2 | 0 |
| Котангенс 105 | 5π/12 | -0.2679 |
| Котангенс 120 | 2π/3 | -0.5774 |
| Котангенс 135 | 3π/4 | -1 |
| Котангенс 140 | 7π/9 | -1.1918 |
| Котангенс 150 | 5π/6 | -1.7321 |
| Котангенс 180 | π | - |
| Котангенс 270 | 3π/2 | 0 |
| Котангенс 360 | 2π |
Если угол больше 90 градусов, нужно помнить, что функции имеют свойство повторяться, поэтому, если ищем тангенс 145 градусов, тогда 180 – 145 = 35 градусов, но уже со знаком «минус», это можно понять по чертежу окружности, где положительное или отрицательное значение абсциссы и ординаты.
Научиться быстро пользоваться таблицами Брадиса и рассчитывать значения треугольника совсем не сложно, главное, уловить суть процесса. Но можно, если это не экзамен по математике, рассчитать функцию котангенса и онлайн на сайте.
Таблица котангенсов Брадиса для углов до 75 градусов
| ctg | 0' | 6' | 12' | 18' | 24' | 30' | 36' | 42' | 48' | 54' | 60' | 1' | 2' | 3' |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ctg | 60' | 54' | 48' | 42' | 36' | 30' | 24' | 18' | 12' | 6' | 0' | 1' | 2' | 3' |
| 0 | 90° | |||||||||||||
| 89° | 0 | 17 | 35 | 52 | 70 | 87 | 105 | 122 | 140 | 157 | 175 | 3 | 6 | 9 |
| 88° | 175 | 192 | 209 | 227 | 244 | 262 | 279 | 297 | 314 | 332 | 349 | 3 | 6 | 9 |
| 87° | 349 | 367 | 384 | 402 | 419 | 437 | 454 | 472 | 489 | 507 | 524 | 3 | 6 | 9 |
| 86° | 524 | 542 | 559 | 577 | 594 | 612 | 629 | 647 | 664 | 682 | 699 | 3 | 6 | 9 |
| 85° | 699 | 717 | 734 | 752 | 769 | 787 | 805 | 822 | 840 | 857 | 0.0875 | 3 | 6 | 9 |
| 84° | 0.0875 | 892 | 910 | 928 | 945 | 963 | 981 | 998 | 1016 | 1033 | 1051 | 3 | 6 | 9 |
| 83° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 3 | 6 | 9 |
| 82° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 3 | 6 | 9 |
| 81° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 3 | 6 | 9 |
| 80° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0.1763 | 3 | 6 | 9 |
| 79° | 0.1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 3 | 6 | 9 |
| 78° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 3 | 6 | 9 |
| 77° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 3 | 6 | 9 |
| 76° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 3 | 6 | 9 |
| 75° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0.2679 | 3 | 6 | 9 |
| 74° | 0.2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 3 | 6 | 9 |
| 73° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 3 | 6 | 9 |
| 72° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 3 | 6 | 10 |
| 71° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 3 | 6 | 10 |
| 70° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0.364 | 3 | 7 | 10 |
| 69° | 0.364 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 3 | 7 | 10 |
| 68° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 3 | 7 | 10 |
| 67° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 3 | 7 | 10 |
| 66° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 3 | 7 | 10 |
| 65° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0.4663 | 4 | 7 | 11 |
| 64° | 0.4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 4 | 7 | 11 |
| 63° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 4 | 7 | 11 |
| 62° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 4 | 7 | 11 |
| 61° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 4 | 8 | 11 |
| 60° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0.5774 | 4 | 8 | 12 |
| 59° | 0.5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 4 | 8 | 12 |
| 58° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 4 | 8 | 12 |
| 57° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 4 | 8 | 12 |
| 56° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 4 | 8 | 13 |
| 55° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0.7002 | 4 | 9 | 13 |
| 54° | 0.7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 4 | 8 | 13 |
| 53° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 5 | 9 | 14° |
| 52° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 5 | 9 | 14 |
| 51° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 5 | 9 | 14 |
| 50° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0.8391 | 5 | 10 | 15 |
| 49° | 0.8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0.8693 | 5 | 10 | 15 |
| 48° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 5 | 10 | 16 |
| 47° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 6 | 11 | 16 |
| 46° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0.9657 | 6 | 11 | 17 |
| 45° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1 | 6 | 11 | 17 |
| 44° | 1 | 35 | 70 | 105 | 141 | 176 | 212 | 247 | 283 | 319 | 355 | 6 | 12 | 18 |
| 43° | 355 | 392 | 428 | 464 | 501 | 538 | 575 | 612 | 649 | 686 | 724 | 6 | 12 | 18 |
| 42° | 724 | 761 | 799 | 837 | 875 | 913 | 951 | 990 | 1028 | 1067 | 1106 | 6 | 13 | 19 |
| 41° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 7 | 13 | 20 |
| 40° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1.1918 | 7 | 14 | 21 |
| 39° | 1.1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 7 | 14 | 22 |
| 38° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 8 | 15 | 23 |
| 37° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 8 | 16 | 24 |
| 36° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 8 | 16 | 25 |
| 35° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1.4281 | 9 | 17 | 26 |
| 34° | 1.4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 9 | 18 | 27 |
| 33° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 10 | 19 | 29 |
| 32° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 10 | 20 | 30 |
| 31° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 11 | 21 | 32 |
| 30° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1.7321 | 11 | 23 | 34 |
| 29° | 1.732 | 1.739 | 1.746 | 1.753 | 1.76 | 1.767 | 1.775 | 1.782 | 1.789 | 1.797 | 1.804 | 1 | 2 | 4 |
| 28° | 1.804 | 1.811 | 1.819 | 1.827 | 1.834 | 1.842 | 1.849 | 1.857 | 1.865 | 1.873 | 1.881 | 1 | 3 | 4 |
| 27° | 1.881 | 1.889 | 1.897 | 1.905 | 1.913 | 1.921 | 1.929 | 1.937 | 1.946 | 1.954 | 1.963 | 1 | 3 | 4 |
| 26° | 1.963 | 1.971 | 1.98 | 1.988 | 1.997 | 2.006 | 2.014 | 2.023 | 2.032 | 2.041 | 2.05 | 1 | 3 | 4 |
| 25° | 2.05 | 2.059 | 2.069 | 2.078 | 2.087 | 2.097 | 2.106 | 2.116 | 2.125 | 2.135 | 2.145 | 2 | 3 | 5 |
| 24° | 2.145 | 2.154 | 2.164 | 2.174 | 2.184 | 2.194 | 2.204 | 2.215 | 2.225 | 2.236 | 2.246 | 2 | 3 | 5 |
| 23° | 2.246 | 2.257 | 2.267 | 2.278 | 2.289 | 2.3 | 2.311 | 2.322 | 2.333 | 2.344 | 2.356 | 2 | 4 | 5 |
| 22° | 2.356 | 2.367 | 2.379 | 2.391 | 2.402 | 2.414 | 2.426 | 2.438 | 2.45 | 2.463 | 2.475 | 2 | 4 | 6 |
| 21° | 2.475 | 2.488 | 2.5 | 2.513 | 2.526 | 2.539 | 2.552 | 2.565 | 2.578 | 2.592 | 2.605 | 2 | 4 | 6 |
| 20° | 2.605 | 2.619 | 2.633 | 2.646 | 2.66 | 2.675 | 2.689 | 2.703 | 2.718 | 2.733 | 2.747 | 2 | 5 | 7 |
| 19° | 2.747 | 2.762 | 2.778 | 2.793 | 2.808 | 2.824 | 2.84 | 2.856 | 2.872 | 2.888 | 2.904 | 3 | 5 | 8 |
| 18° | 2.904 | 2.921 | 2.937 | 2.954 | 2.971 | 2.989 | 3.006 | 3.024 | 3.042 | 3.06 | 3.078 | 3 | 6 | 9 |
| 17° | 3.078 | 3.096 | 3.115 | 3.133 | 3.152 | 3.172 | 3.191 | 3.211 | 3.23 | 3.251 | 3.271 | 3 | 6 | 10 |
| 16° | 3.271 | 3.291 | 3.312 | 3.333 | 3.354 | 3.376 | 3 | 7 | 10 | |||||
| 3.398 | 3.42 | 3.442 | 3.465 | 3.487 | 4 | 7 | 11 | |||||||
| 15° | 3.487 | 3.511 | 3.534 | 3.558 | 3.582 | 3.606 | 4 | 8 | 12 | |||||
| 3.63 | 3.655 | 3.681 | 3.706 | 3.732 | 4 | 8 | 13 | |||||||
| 14° | 3.732 | 3.758 | 3.785 | 3.812 | 3.839 | 3.867 | 4 | 9 | 13 | |||||
| 3.895 | 3.923 | 3.952 | 3.981 | 4.011 | 5 | 10 | 14 |
Таблица котангенсов Брадиса для углов, близких к 90 градусам
| ctg | 0' | 1' | 2' | 3' | 4' | 5' | 6' | 7' | 8' | 9' | 10' |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ctg | 10' | 9' | 8' | 7' | 6' | 5' | 4' | 3' | 2' | 1' | 0' |
| 50' | 4.011 | 4.016 | 4.021 | 4.026 | 4.031 | 4.036 | 4.041 | 4.046 | 4.051 | 4.056 | 4.061 |
| 40' | 4.061 | 4.066 | 4.071 | 4.076 | 4.082 | 4.087 | 4.092 | 4.097 | 4.102 | 4.107 | 4.113 |
| 30' | 4.113 | 4.118 | 4.123 | 4.128 | 4.134 | 4.139 | 4.144 | 4.149 | 4.155 | 4.16 | 4.165 |
| 20' | 4.165 | 4.171 | 4.176 | 4.181 | 4.187 | 4.192 | 4.198 | 4.203 | 4.208 | 4.214 | 4.219 |
| 10' | 4.219 | 4.225 | 4.23 | 4.236 | 4.241 | 4.247 | 4.252 | 4.258 | 4.264 | 4.269 | 4.275 |
| 13°00' | 4.275 | 4.28 | 4.286 | 4.292 | 4.297 | 4.303 | 4.309 | 4.314 | 4.32 | 4.326 | 4.331 |
| 50' | 4.331 | 4.337 | 4.343 | 4.349 | 4.355 | 4.36 | 4.366 | 4.372 | 4.378 | 4.384 | 4.39 |
| 40' | 4.39 | 4.396 | 4.402 | 4.407 | 4.413 | 4.419 | 4.425 | 4.431 | 4.437 | 4.443 | 4.449 |
| 30' | 4.449 | 4.455 | 4.462 | 4.468 | 4.474 | 4.48 | 4.486 | 4.492 | 4.498 | 4.505 | 4.511 |
| 20' | 4.511 | 4.517 | 4.523 | 4.529 | 4.536 | 4.542 | 4.548 | 4.555 | 4.561 | 4.567 | 4.574 |
| 10' | 4.574 | 4.58 | 4.586 | 4.593 | 4.599 | 4.606 | 4.612 | 4.619 | 4.625 | 4.632 | 4.638 |
| 12°00' | 4.638 | 4.645 | 4.651 | 4.658 | 4.665 | 4.671 | 4.678 | 4.685 | 4.691 | 4.698 | 4.705 |
| 50' | 4.705 | 4.711 | 4.718 | 4.725 | 4.732 | 4.739 | 4.745 | 4.752 | 4.759 | 4.766 | 4.773 |
| 40' | 4.773 | 4.78 | 4.787 | 4.794 | 4.801 | 4.808 | 4.815 | 4.822 | 4.829 | 4.836 | 4.843 |
| 30' | 4.843 | 4.85 | 4.857 | 4.864 | 4.872 | 4.879 | 4.886 | 4.893 | 4.901 | 4.908 | 4.915 |
| 20' | 4.915 | 4.922 | 4.93 | 4.937 | 4.945 | 4.952 | 4.959 | 4.967 | 4.974 | 4.982 | 4.989 |
| 10' | 4.989 | 4.997 | 5.005 | 5.012 | 5.02 | 5.027 | 5.035 | 5.043 | 5.05 | 5.058 | 5.066 |
| 11°00' | 5.066 | 5.074 | 5.081 | 5.089 | 5.097 | 5.105 | 5.113 | 5.121 | 5.129 | 5.137 | 5.145 |
| 50' | 5.145 | 5.153 | 5.161 | 5.169 | 5.177 | 5.185 | 5.193 | 5.201 | 5.209 | 5.217 | 5.226 |
| 40' | 5.226 | 5.234 | 5.242 | 5.25 | 5.259 | 5.267 | 5.276 | 5.284 | 5.292 | 5.301 | 5.309 |
| 30' | 5.309 | 5.318 | 5.326 | 5.335 | 5.343 | 5.352 | 5.361 | 5.369 | 5.378 | 5.387 | 5.396 |
| 20' | 5.396 | 5.404 | 5.413 | 5.422 | 5.431 | 5.44 | 5.449 | 5.458 | 5.466 | 5.475 | 5.485 |
| 10' | 5.485 | 5.494 | 5.503 | 5.512 | 5.521 | 5.53 | 5.539 | 5.549 | 5.558 | 5.567 | 5.576 |
| 10°00' | 5.576 | 5.586 | 5.595 | 5.605 | 5.614 | 5.623 | 5.633 | 5.642 | 5.652 | 5.662 | 5.671 |
| 50' | 5.671 | 5.681 | 5.691 | 5.7 | 5.71 | 5.72 | 5.73 | 5.74 | 5.749 | 5.759 | 5.769 |
| 40' | 5.769 | 5.779 | 5.789 | 5.799 | 5.81 | 5.82 | 5.83 | 5.84 | 5.85 | 5.861 | 5.871 |
| 30' | 5.871 | 5.881 | 5.892 | 5.902 | 5.912 | 5.923 | 5.933 | 5.944 | 5.954 | 5.965 | 5.976 |
| 20' | 5.976 | 5.986 | 5.997 | 6.008 | 6.019 | 6.03 | 6.041 | 6.051 | 6.062 | 6.073 | 6.084 |
| 10' | 6.084 | 6.096 | 6.107 | 6.118 | 6.129 | 6.14 | 6.152 | 6.163 | 6.174 | 6.186 | 6.197 |
| 9°00' | 6.197 | 6.209 | 6.22 | 6.232 | 6.243 | 6.255 | 6.267 | 6.278 | 6.29 | 6.302 | 6.314 |
| 50' | 6.314 | 6.326 | 6.338 | 6.35 | 6.362 | 6.374 | 6.386 | 6.398 | 6.41 | 6.423 | 6.435 |
| 40' | 6.435 | 6.447 | 6.46 | 6.472 | 6.485 | 6.497 | 6.51 | 6.522 | 6.535 | 6.548 | 6.561 |
| 30' | 6.561 | 6.573 | 6.586 | 6.599 | 6.612 | 6.625 | 6.638 | 6.651 | 6.665 | 6.678 | 6.691 |
| 20' | 6.691 | 6.704 | 6.718 | 6.731 | 6.745 | 6.758 | 6.772 | 6.786 | 6.799 | 6.813 | 6.827 |
| 10' | 6.827 | 6.841 | 6.855 | 6.869 | 6.883 | 6.897 | 6.911 | 6.925 | 6.94 | 6.954 | 6.968 |
| 8°00' | 6.968 | 6.983 | 6.997 | 7.012 | 7.026 | 7.041 | 7.056 | 7.071 | 7.085 | 7.1 | 7.115 |
| 50' | 7.115 | 7.13 | 7.146 | 7.161 | 7.176 | 7.191 | 7.207 | 7.222 | 7.238 | 7.253 | 7.269 |
| 40' | 7.269 | 7.284 | 7.3 | 7.316 | 7.332 | 7.348 | 7.363 | 7.38 | 7.396 | 7.412 | 7.429 |
| 30' | 7.429 | 7.445 | 7.462 | 7.478 | 7.495 | 7.511 | 7.528 | 7.545 | 7.562 | 7.579 | 7.596 |
| 20' | 7.596 | 7.613 | 7.63 | 7.647 | 7.665 | 7.682 | 7.7 | 7.717 | 7.735 | 7.753 | 7.77 |
| 10' | 7.77 | 7.788 | 7.806 | 7.824 | 7.842 | 7.861 | 7.879 | 7.897 | 7.916 | 7.934 | 7.953 |
| 7°00' | 7.953 | 7.972 | 7.991 | 8.009 | 8.028 | 8.048 | 8.067 | 8.086 | 8.105 | 8.125 | 8.144 |
| 50' | 8.144 | 8.164 | 8.184 | 8.204 | 8.223 | 8.243 | 8.264 | 8.284 | 8.304 | 8.324 | 8.345 |
| 40' | 8.345 | 8.366 | 8.386 | 8.407 | 8.428 | 8.449 | 8.47 | 8.491 | 8.513 | 8.534 | 8.556 |
| 30' | 8.556 | 8.577 | 8.599 | 8.621 | 8.643 | 8.665 | 8.687 | 8.709 | 8.732 | 8.754 | 8.777 |
| 20' | 8.777 | 8.8 | 8.823 | 8.846 | 8.869 | 8.892 | 8.915 | 8.939 | 8.962 | 8.986 | 9.01 |
| 10' | 9.01 | 9.034 | 9.058 | 9.082 | 9.106 | 9.131 | 9.156 | 9.18 | 9.205 | 9.23 | 9.255 |
| 6°00' | 9.255 | 9.281 | 9.306 | 9.332 | 9.357 | 9.383 | 9.409 | 9.435 | 9.461 | 9.488 | 9.514 |
| 50' | 9.514 | 9.541 | 9.568 | 9.595 | 9.622 | 9.649 | 9.677 | 9.704 | 9.732 | 9.76 | 9.788 |
| 40' | 9.788 | 9.816 | 9.845 | 9.873 | 9.902 | 9.931 | 9.96 | 9.989 | 10.02 | 10.05 | 10.08 |
| 30' | 10.08 | 10.11 | 10.14 | 10.17 | 10.2 | 10.23 | 10.26 | 10.29 | 10.32 | 10.35 | 10.39 |
| 20' | 10.39 | 10.42 | 10.45 | 10.48 | 10.51 | 10.55 | 10.58 | 10.61 | 10.64 | 10.68 | 10.71 |
| 10' | 10.71 | 10.75 | 10.78 | 10.81 | 10.85 | 10.88 | 10.92 | 10.95 | 10.99 | 11.02 | 11.06 |
| 5°00' | 11.06 | 11.1 | 11.13 | 11.17 | 11.2 | 11.24 | 11.28 | 11.32 | 11.35 | 11.39 | 11.43 |
| 50' | 11.43 | 11.47 | 11.51 | 11.55 | 11.59 | 11.62 | 11.66 | 11.7 | 11.74 | 11.79 | 11.83 |
| 40' | 11.83 | 11.87 | 11.91 | 11.95 | 11.99 | 12.03 | 12.08 | 12.12 | 12.16 | 12.21 | 12.25 |
| 30' | 12.25 | 12.29 | 12.34 | 12.38 | 12.43 | 12.47 | 12.52 | 12.57 | 12.61 | 12.66 | 12.71 |
| 20' | 12.71 | 12.75 | 12.8 | 12.85 | 12.9 | 12.95 | 13 | 13.05 | 13.1 | 13.15 | 13.2 |
| 10' | 13.2 | 13.25 | 13.3 | 13.35 | 13.4 | 13.46 | 13.51 | 13.56 | 13.62 | 13.67 | 13.73 |
| 4°00' | 13.73 | 13.78 | 13.84 | 13.89 | 13.95 | 14.01 | 14.07 | 14.12 | 14.18 | 14.24 | 14.3 |
| 50' | 14.3 | 14.36 | 14.42 | 14.48 | 14.54 | 14.61 | 14.67 | 14.73 | 14.8 | 14.86 | 14.92 |
| 40' | 14.92 | 14.99 | 15.06 | 15.12 | 15.19 | 15.26 | 15.33 | 15.39 | 15.46 | 15.53 | 15.6 |
| 30' | 15.6 | 15.68 | 15.75 | 15.82 | 15.89 | 15.97 | 16.04 | 16.12 | 16.2 | 16.27 | 16.35 |
| 20' | 16.35 | 16.43 | 16.51 | 16.59 | 16.67 | 16.75 | 16.83 | 16.92 | 17 | 17.08 | 17.17 |
| 10' | 17.17 | 17.26 | 17.34 | 17.43 | 17.52 | 17.61 | 17.7 | 17.79 | 17.89 | 17.98 | 18.07 |
| 3°00' | 18.07 | 18.17 | 18.27 | 18.37 | 18.46 | 18.56 | 18.67 | 18.77 | 18.87 | 18.98 | 19.08 |
| 50' | 19.08 | 19.19 | 19.3 | 19.41 | 19.52 | 19.63 | 19.74 | 19.85 | 19.97 | 20.09 | 20.21 |
| 40' | 20.21 | 20.33 | 20.45 | 20.57 | 20.69 | 20.82 | 20.95 | 21.07 | 21.2 | 21.34 | 21.47 |
| 30' | 21.47 | 21.61 | 21.74 | 21.88 | 22.02 | 22.16 | 22.31 | 22.45 | 22.6 | 22.75 | 22.9 |
| 20' | 22.9 | 23.06 | 23.21 | 23.37 | 23.53 | 23.69 | 23.86 | 24.03 | 24.2 | 24.37 | 24.54 |
| 10' | 24.54 | 24.72 | 24.9 | 25.08 | 25.26 | 25.45 | 25.64 | 25.83 | 26.03 | 26.23 | 26.43 |
| 2°00' | 26.43 | 26.64 | 26.84 | 27.06 | 27.27 | 27.49 | 27.71 | 27.94 | 28.17 | 28.4 | 28.64 |
| 50' | 28.64 | 28.88 | 29.12 | 29.37 | 29.62 | 29.88 | 30.14 | 30.41 | 30.68 | 30.96 | 31.24 |
| 40' | 31.24 | 31.53 | 31.82 | 32.12 | 32.42 | 32.73 | 33.05 | 33.37 | 33.69 | 34.03 | 34.37 |
| 30' | 34.37 | 34.72 | 35.07 | 35.43 | 35.8 | 36.18 | 36.56 | 36.96 | 37.36 | 37.77 | 38.19 |
| 20' | 38.19 | 38.62 | 39.06 | 39.51 | 39.97 | 40.44 | 40.92 | 41.41 | 41.92 | 42.43 | 42.96 |
| 10' | 42.96 | 43.51 | 44.07 | 44.64 | 45.23 | 45.83 | 46.45 | 47.09 | 47.74 | 48.41 | 49.1 |
| 1°00' | 49.1 | 49.82 | 50.55 | 51.3 | 52.08 | 52.88 | 53.71 | 54.56 | 55.44 | 56.35 | 57.29 |
| 50' | 57.29 | 58.26 | 59.27 | 60.31 | 61.38 | 62.5 | 63.66 | 64.86 | 66.11 | 67.4 | 68.75 |
| 40' | 68.75 | 70.15 | 71.62 | 73.14 | 74.73 | 76.39 | 78.13 | 79.94 | 81.85 | 83.84 | 85.94 |
| 30' | 85.94 | 88.14 | 90.46 | 92.91 | 95.49 | 98.22 | 101.1 | 104.2 | 107.4 | 110.9 | 114.6 |
| 20' | 114.6 | 118.5 | 122.8 | 127.3 | 132.2 | 137.5 | 143.2 | 149.5 | 156.3 | 163.7 | 171.9 |
| 10' | 171.9 | 180.9 | 191 | 202.2 | 214.9 | 229.2 | 245.6 | 264.4 | 286.5 | 312.5 | 343.8 |
| 0°00' | 343.8 | 382 | 429.7 | 491.1 | 573 | 687.5 | 859.4 | 1146 | 1719 | 3438 |