Содержание статьи тангенс угла
- Тригонометрические функции, что это такое и их значение в изучении геометрии
- Онлайн калькулятор расчета тангенса угла
- Применение функции тангенса для решения задач
- Таблица тангенсов Брадиса для углов от 0 до 75 градусов
- Таблица тангенсов Брадиса для углов близких к 90 градусов
Из четырёх наиболее используемых тригонометрических таблиц в справочнике Брадиса является ТАБЛИЦА ТАНГЕНСОВ. И тангенс и котангенс – это производные от синуса и косинуса и очень удобно, когда есть готовые рассчитанные значения для этих величин
Тригонометрические функции, что это такое и их значение в изучении геометрии
В геометрии особую роль имеют тригонометрические функции, при помощи которых определяют, как относятся между собой стороны и углы прямоугольного треугольника. Конечно, тригонометрия не стоит на месте и со времен Евклида она намного шагнула вперёд и теперь может эти функции могут выражаться через решение дифференциальных уравнений.
В данный момент используются шесть обозначений для основных тригонометрических функций, причем четыре функции из шести, они стоят в ряду последними, можно определять не только с помощью геометрии.
Синус (sin) ![]()
Косинус (cos) ![]()
Тангенс (tg/tan) ![]()
Котангенс (ctg/cot) ![]()
Секанс (sec) ![]()
Косеканс (cosec/csc) ![]() .
.
Рассмотрим сам прямоугольный треугольник, обозначения его сторон и углов во всех справочниках, как обычно, стандартные, какой бы стороной он не лежал бы на плоскости.
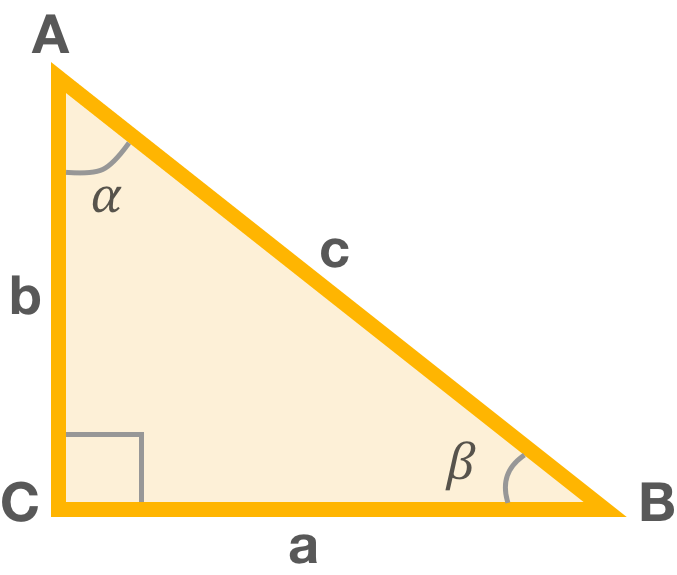
В этом треугольнике различают три угла, обозначаемые α, β, γ, при этом γ всегда 90°. Сторона, лежащая напротив прямого угла γ, называется гипотенузой, она обозначается буквой С. Угол α, с него начинаются все расчеты, находится напротив стороны а / ВС/, называемой противолежащей к этому углу, и сторона b /АС/, которая находится рядом, подлежит к этому углу и называется прилежащей.
По Евклидовой теории, которая верна до сих пор (и будет верна всегда), суммы углов такого треугольника, который находится в одной плоскости, будет равна 180 или числу π. И значение любого угла будут находиться в пределах между 0 и π /2.
Тогда тригонометрические функции можно выразить через размеры сторон этого треугольника. Так как угол α является первым и в греческом алфавите и в нашем треугольнике, начинаем знакомство с функциями через этот угол.
- Синус α выражается через отношение катета, который лежит напротив этого угла, к гипотенузе нашего треугольника, то есть sin α = а: с.
- Косинус α выражается через отношение катета, который прилежит к углу α, и гипотенузы с, cos α = b: с. Кстати, sin β = α: с, что позволяет принять то, что sin α равен cos β и следовательно sin β равен cos α.
- Тангенс α равен частному от отношения противолежащего катета а к катету прилежащему b: tg α = а : b.
- Котангенс угла α в соответствии равен ctg α = b : а.
- Секанс угла α составляет отношение гипотенузы треугольника к катету, прилежащему к этому углу sec α = c : b.
- Косеканс угла α составляет отношение гипотенузы треугольника к катету, который противостоит углу, cosecα = с : a.
Эти функции можно выразить и через окружность путем задания системы координат. Задаем систему координат с центом в точке О. Угол, на который поворачивается отрезок ОА, изображенный на чертеже, будем считать произвольным, назовем его θ.
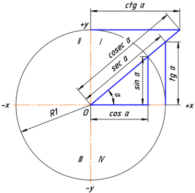
Тогда тангенсом этого угла θсчитается отношение ординаты точки А на окружности к её абсциссе. Следовательно, если ctg α = b : а, а АС = sin θ, ОС = cos θ, то tgθ = sin θ : cos θ. Аналогично получаем ctg θ = cos θ : sin θ или 1 : tgθ.
Онлайн калькулятор расчета тангенса угла
Применение функции тангенса для решения задач
Что бы научиться пользоваться этой функцией, Нужно попробовать решить несколько примеров по применению этой функции.
Пример: есть два катета ВС = 7 см и АС = 12 см. Нам нужно узнать все остальные данные о треугольнике.
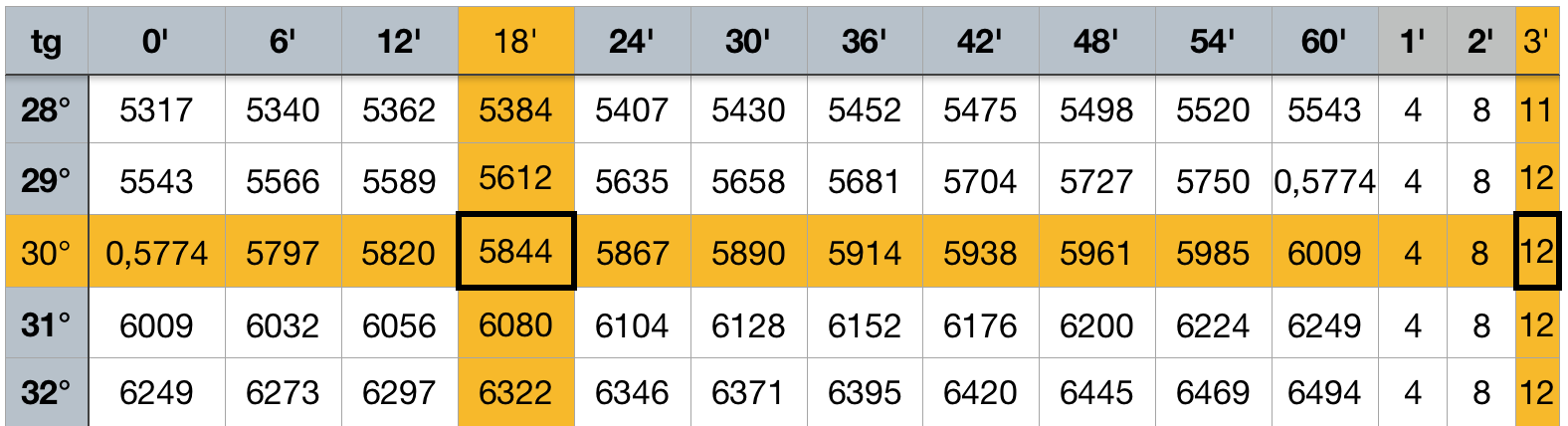
Первая формула, это tg α = а : b. тогда tg α = 7 :12= 0, 5833, далее для нахождения угла α используем таблицы Брадиса. На пересечении градусов и минут находим ближайшее значение угла – 0,5844, соответствующее 30° и 18′.
Находим ближайшую поправку, разную 3′. Отнимаем ее от нашего угла и получаем угол α = 30° 15′. Второй угол находим, исходя из того, что сумма всех углов должна быть не больше 180°, а угол γ = 90° по условию. Тогда угол β = 90° – 30° 15′= 59°45′.
Нам осталось найти гипотенузу с.
Можем найти её через sin α, который равен а: с, тогда с = а : sin α.
Находим sin α через таблицу Брадиса. Ближайшее значение 30° 36′, будет 0,5060, тогда не хватает 3′, Что по полям поправок равно 0,0008. Добавляем это число к найденному: 0, 5060 + 0,0008 = 0,5068. Подставляем это значение в формулу, с = 7:0,5068, с = 13, 8 см. Задача решена.
Можно искать значение углов через значение числа π, которое равно 180°. Тогда наиболее популярные углы, такие, как тангенс 30 градусов, тангенс 0 градусов, тангенс 60 градусов, тангенс 90 градусов, тангенс 45 градусов, тангенс 15 градусов, тангенс 75 градусов можно рассматривать намного проще. Нужно знать, что тангенс 0 градусов равен 0, а тангенс 90 градусов не имеет конкретного значения.
Можно найти тангенс угла 5 градусов, который равен 0, 0875 и добавлять или отнимать от наиболее часто встречающихся углов. Например угол 45 градусов, его тангенс равен 1, тогда тангенс угла 50 градусов будет равен 1, 0875. Тангенс 35 градусов можно рассчитать путем добавления к тангенсу 30 градусов угол 5 градусов, а тангенс 10 градусов это удвоение угла 5 градусов.
Для удобства есть рассчитанная таблица основных углов через значение π.
| Значение угла α (градусов) | Значение угла α в радианах | tg (тангенс) |
|---|---|---|
| Тангенс 0 | 0 | 0 |
| Тангенс 15 | π/12 | 0.2679 |
| Тангенс 30 | π/6 | 0.5774 |
| Тангенс 45 | π/4 | 1 |
| Тангенс 50 | 5π/18 | 5114 |
| Тангенс 60 | π/3 | 1.7321 |
| Тангенс 65 | 13π/36 | 2.1445 |
| Тангенс 70 | 7π/18 | 2.7475 |
| Тангенс 75 | 5π/12 | 3.7321 |
| Тангенс 90 | π/2 | - |
| Тангенс 105 | 5π/12 | -3.7321 |
| Тангенс 120 | 2π/3 | -1.7321 |
| Тангенс 135 | 3π/4 | -1 |
| Тангенс 140 | 7π/9 | -0.8391 |
| Тангенс 150 | 5π/6 | -0.5774 |
| Тангенс 180 | π | 0 |
| Тангенс 270 | 3π/2 | - |
| Тангенс 360 | 2π | 0 |
Если угол больше 90 градусов, нужно помнить, что функции имеют свойство повторяться, поэтому, если ищем тангенс 145 градусов, тогда 180 – 145 = 35 градусов, но уже со знаком «минус», это можно понять по чертежу окружности, где положительное или отрицательное значение абсциссы и ординаты. Научиться быстро пользоваться таблицами Брадиса и рассчитывать значения треугольника совсем не сложно, главное, уловить суть процесса.
Таблица тангенсов Брадиса для углов от 0 до 75 градусов
| tg | 0' | 6' | 12' | 18' | 24' | 30' | 36' | 42' | 48' | 54' | 60' | 1' | 2' | 3' |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 74° | 3.487 | 3.511 | 3.534 | 3.558 | 3.582 | 3.606 | 4 | 8 | 12 | |||||
| 73° | 3.271 | 3.291 | 3.312 | 3.333 | 3.354 | 3.376 | - | - | - | - | - | 3 | 7 | 10 |
| 75° | 3.732 | 3.758 | 3.785 | 3.812 | 3.839 | 3.867 | - | - | - | - | - | 4 | 9 | 13 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1 | 6 | 11 | 17 |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0.9657 | 6 | 11 | 17 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 6 | 11 | 16 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 5 | 10 | 16 |
| 40° | 0.8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0.8693 | 5 | 10 | 15 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0.8391 | 5 | 10 | 15 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 5 | 9 | 14 |
| 37° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 5 | 9 | 14 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 5 | 9 | 14° |
| 35° | 0.7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 4 | 8 | 13 |
| 59° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1.7321 | 11 | 23 | 34 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0.7002 | 4 | 9 | 13 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 4 | 8 | 13 |
| 58° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 11 | 21 | 32 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 4 | 8 | 12 |
| 30° | 0.5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 4 | 8 | 12 |
| 57° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 10 | 20 | 30 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0.5774 | 4 | 8 | 12 |
| 28° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 4 | 8 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 4 | 7 | 11 |
| 56° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 10 | 19 | 29 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 4 | 7 | 11 |
| 25° | 0.4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 4 | 7 | 11 |
| 55° | 1.4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 9 | 18 | 27 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0.4663 | 4 | 7 | 11 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 3 | 7 | 10 |
| 22° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 3 | 7 | 10 |
| 54° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1.4281 | 9 | 17 | 26 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 3 | 7 | 10 |
| 20° | 0.364 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 3 | 7 | 10 |
| 53° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 8 | 16 | 25 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0.364 | 3 | 7 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 3 | 6 | 10 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 3 | 6 | 10 |
| 52° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 8 | 16 | 24 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 3 | 6 | 9 |
| 15° | 0.2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 3 | 6 | 9 |
| 51° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 8 | 15 | 23 |
| 14° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0.2679 | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 3 | 6 | 9 |
| 50° | 1.1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 7 | 14 | 22 |
| 11° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 3 | 6 | 9 |
| 10° | 0.1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 3 | 6 | 9 |
| 49° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1.1918 | 7 | 14 | 21 |
| 9° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0.1763 | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 3 | 6 | 9 |
| 48° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 7 | 13 | 20 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 3 | 6 | 9 |
| 5° | 0.0875 | 892 | 910 | 928 | 945 | 963 | 981 | 998 | 1016 | 1033 | 1051 | 3 | 6 | 9 |
| 47° | 724 | 761 | 799 | 837 | 875 | 913 | 951 | 990 | 1028 | 1067 | 1106 | 6 | 13 | 19 |
| 4° | 699 | 717 | 734 | 752 | 769 | 787 | 805 | 822 | 840 | 857 | 0.0875 | 3 | 6 | 9 |
| 3° | 524 | 542 | 559 | 577 | 594 | 612 | 629 | 647 | 664 | 682 | 699 | 3 | 6 | 9 |
| 46° | 355 | 392 | 428 | 464 | 501 | 538 | 575 | 612 | 649 | 686 | 724 | 6 | 12 | 18 |
| 2° | 349 | 367 | 384 | 402 | 419 | 437 | 454 | 472 | 489 | 507 | 524 | 3 | 6 | 9 |
| 1° | 175 | 192 | 209 | 227 | 244 | 262 | 279 | 297 | 314 | 332 | 349 | 3 | 6 | 9 |
| 45° | 1 | 35 | 70 | 105 | 141 | 176 | 212 | 247 | 283 | 319 | 355 | 6 | 12 | 18 |
| 0° | 0 | 17 | 35 | 52 | 70 | 87 | 105 | 122 | 140 | 157 | 175 | 3 | 6 | 9 |
| tg | 60' | 54' | 48' | 42' | 36' | 30' | 24' | 18' | 12' | 6' | 0' | 1' | 2' | 3' |
| - | - | - | - | - | - | 3.895 | 3.923 | 3.952 | 3.981 | 4.011 | 5 | 10 | 14 | |
| - | - | - | - | - | - | 3.63 | 3.655 | 3.681 | 3.706 | 3.732 | 4 | 8 | 13 | |
| - | - | - | - | - | - | 3.398 | 3.42 | 3.442 | 3.465 | 3.487 | 4 | 7 | 11 | |
| 72° | 3.078 | 3.096 | 3.115 | 3.133 | 3.152 | 3.172 | 3.191 | 3.211 | 3.23 | 3.251 | 3.271 | 3 | 6 | 10 |
| 71° | 2.904 | 2.921 | 2.937 | 2.954 | 2.971 | 2.989 | 3.006 | 3.024 | 3.042 | 3.06 | 3.078 | 3 | 6 | 9 |
| 70° | 2.747 | 2.762 | 2.778 | 2.793 | 2.808 | 2.824 | 2.84 | 2.856 | 2.872 | 2.888 | 2.904 | 3 | 5 | 8 |
| 69° | 2.605 | 2.619 | 2.633 | 2.646 | 2.66 | 2.675 | 2.689 | 2.703 | 2.718 | 2.733 | 2.747 | 2 | 5 | 7 |
| 68° | 2.475 | 2.488 | 2.5 | 2.513 | 2.526 | 2.539 | 2.552 | 2.565 | 2.578 | 2.592 | 2.605 | 2 | 4 | 6 |
| 67° | 2.356 | 2.367 | 2.379 | 2.391 | 2.402 | 2.414 | 2.426 | 2.438 | 2.45 | 2.463 | 2.475 | 2 | 4 | 6 |
| 66° | 2.246 | 2.257 | 2.267 | 2.278 | 2.289 | 2.3 | 2.311 | 2.322 | 2.333 | 2.344 | 2.356 | 2 | 4 | 5 |
| 65° | 2.145 | 2.154 | 2.164 | 2.174 | 2.184 | 2.194 | 2.204 | 2.215 | 2.225 | 2.236 | 2.246 | 2 | 3 | 5 |
| 64° | 2.05 | 2.059 | 2.069 | 2.078 | 2.087 | 2.097 | 2.106 | 2.116 | 2.125 | 2.135 | 2.145 | 2 | 3 | 5 |
| 63° | 1.963 | 1.971 | 1.98 | 1.988 | 1.997 | 2.006 | 2.014 | 2.023 | 2.032 | 2.041 | 2.05 | 1 | 3 | 4 |
| 62° | 1.881 | 1.889 | 1.897 | 1.905 | 1.913 | 1.921 | 1.929 | 1.937 | 1.946 | 1.954 | 1.963 | 1 | 3 | 4 |
| 61° | 1.804 | 1.811 | 1.819 | 1.827 | 1.834 | 1.842 | 1.849 | 1.857 | 1.865 | 1.873 | 1.881 | 1 | 3 | 4 |
| 60° | 1.732 | 1.739 | 1.746 | 1.753 | 1.76 | 1.767 | 1.775 | 1.782 | 1.789 | 1.797 | 1.804 | 1 | 2 | 4 |
| 0 | 90° |
Таблица тангенсов Брадиса для углов близких к 90 градусов
| tg | 0' | 1' | 2' | 3' | 4' | 5' | 6' | 7' | 8' | 9' | 10' |
|---|---|---|---|---|---|---|---|---|---|---|---|
| tg | 10' | 9' | 8' | 7' | 6' | 5' | 4' | 3' | 2' | 1' | 0' |
| 76°00' | 4.011 | 4.016 | 4.021 | 4.026 | 4.031 | 4.036 | 4.041 | 4.046 | 4.051 | 4.056 | 4.061 |
| 10' | 4.061 | 4.066 | 4.071 | 4.076 | 4.082 | 4.087 | 4.092 | 4.097 | 4.102 | 4.107 | 4.113 |
| 20' | 4.113 | 4.118 | 4.123 | 4.128 | 4.134 | 4.139 | 4.144 | 4.149 | 4.155 | 4.16 | 4.165 |
| 30' | 4.165 | 4.171 | 4.176 | 4.181 | 4.187 | 4.192 | 4.198 | 4.203 | 4.208 | 4.214 | 4.219 |
| 40' | 4.219 | 4.225 | 4.23 | 4.236 | 4.241 | 4.247 | 4.252 | 4.258 | 4.264 | 4.269 | 4.275 |
| 50' | 4.275 | 4.28 | 4.286 | 4.292 | 4.297 | 4.303 | 4.309 | 4.314 | 4.32 | 4.326 | 4.331 |
| 77°00' | 4.331 | 4.337 | 4.343 | 4.349 | 4.355 | 4.36 | 4.366 | 4.372 | 4.378 | 4.384 | 4.39 |
| 10' | 4.39 | 4.396 | 4.402 | 4.407 | 4.413 | 4.419 | 4.425 | 4.431 | 4.437 | 4.443 | 4.449 |
| 20' | 4.449 | 4.455 | 4.462 | 4.468 | 4.474 | 4.48 | 4.486 | 4.492 | 4.498 | 4.505 | 4.511 |
| 30' | 4.511 | 4.517 | 4.523 | 4.529 | 4.536 | 4.542 | 4.548 | 4.555 | 4.561 | 4.567 | 4.574 |
| 40' | 4.574 | 4.58 | 4.586 | 4.593 | 4.599 | 4.606 | 4.612 | 4.619 | 4.625 | 4.632 | 4.638 |
| 50' | 4.638 | 4.645 | 4.651 | 4.658 | 4.665 | 4.671 | 4.678 | 4.685 | 4.691 | 4.698 | 4.705 |
| 78°00' | 4.705 | 4.711 | 4.718 | 4.725 | 4.732 | 4.739 | 4.745 | 4.752 | 4.759 | 4.766 | 4.773 |
| 10' | 4.773 | 4.78 | 4.787 | 4.794 | 4.801 | 4.808 | 4.815 | 4.822 | 4.829 | 4.836 | 4.843 |
| 20' | 4.843 | 4.85 | 4.857 | 4.864 | 4.872 | 4.879 | 4.886 | 4.893 | 4.901 | 4.908 | 4.915 |
| 30' | 4.915 | 4.922 | 4.93 | 4.937 | 4.945 | 4.952 | 4.959 | 4.967 | 4.974 | 4.982 | 4.989 |
| 40' | 4.989 | 4.997 | 5.005 | 5.012 | 5.02 | 5.027 | 5.035 | 5.043 | 5.05 | 5.058 | 5.066 |
| 50' | 5.066 | 5.074 | 5.081 | 5.089 | 5.097 | 5.105 | 5.113 | 5.121 | 5.129 | 5.137 | 5.145 |
| 79°00' | 5.145 | 5.153 | 5.161 | 5.169 | 5.177 | 5.185 | 5.193 | 5.201 | 5.209 | 5.217 | 5.226 |
| 10' | 5.226 | 5.234 | 5.242 | 5.25 | 5.259 | 5.267 | 5.276 | 5.284 | 5.292 | 5.301 | 5.309 |
| 20' | 5.309 | 5.318 | 5.326 | 5.335 | 5.343 | 5.352 | 5.361 | 5.369 | 5.378 | 5.387 | 5.396 |
| 30' | 5.396 | 5.404 | 5.413 | 5.422 | 5.431 | 5.44 | 5.449 | 5.458 | 5.466 | 5.475 | 5.485 |
| 40' | 5.485 | 5.494 | 5.503 | 5.512 | 5.521 | 5.53 | 5.539 | 5.549 | 5.558 | 5.567 | 5.576 |
| 50' | 5.576 | 5.586 | 5.595 | 5.605 | 5.614 | 5.623 | 5.633 | 5.642 | 5.652 | 5.662 | 5.671 |
| 80°00' | 5.671 | 5.681 | 5.691 | 5.7 | 5.71 | 5.72 | 5.73 | 5.74 | 5.749 | 5.759 | 5.769 |
| 10' | 5.769 | 5.779 | 5.789 | 5.799 | 5.81 | 5.82 | 5.83 | 5.84 | 5.85 | 5.861 | 5.871 |
| 20' | 5.871 | 5.881 | 5.892 | 5.902 | 5.912 | 5.923 | 5.933 | 5.944 | 5.954 | 5.965 | 5.976 |
| 30' | 5.976 | 5.986 | 5.997 | 6.008 | 6.019 | 6.03 | 6.041 | 6.051 | 6.062 | 6.073 | 6.084 |
| 40' | 6.084 | 6.096 | 6.107 | 6.118 | 6.129 | 6.14 | 6.152 | 6.163 | 6.174 | 6.186 | 6.197 |
| 50' | 6.197 | 6.209 | 6.22 | 6.232 | 6.243 | 6.255 | 6.267 | 6.278 | 6.29 | 6.302 | 6.314 |
| 81°00' | 6.314 | 6.326 | 6.338 | 6.35 | 6.362 | 6.374 | 6.386 | 6.398 | 6.41 | 6.423 | 6.435 |
| 10' | 6.435 | 6.447 | 6.46 | 6.472 | 6.485 | 6.497 | 6.51 | 6.522 | 6.535 | 6.548 | 6.561 |
| 20' | 6.561 | 6.573 | 6.586 | 6.599 | 6.612 | 6.625 | 6.638 | 6.651 | 6.665 | 6.678 | 6.691 |
| 30' | 6.691 | 6.704 | 6.718 | 6.731 | 6.745 | 6.758 | 6.772 | 6.786 | 6.799 | 6.813 | 6.827 |
| 40' | 6.827 | 6.841 | 6.855 | 6.869 | 6.883 | 6.897 | 6.911 | 6.925 | 6.94 | 6.954 | 6.968 |
| 50' | 6.968 | 6.983 | 6.997 | 7.012 | 7.026 | 7.041 | 7.056 | 7.071 | 7.085 | 7.1 | 7.115 |
| 82°00' | 7.115 | 7.13 | 7.146 | 7.161 | 7.176 | 7.191 | 7.207 | 7.222 | 7.238 | 7.253 | 7.269 |
| 10' | 7.269 | 7.284 | 7.3 | 7.316 | 7.332 | 7.348 | 7.363 | 7.38 | 7.396 | 7.412 | 7.429 |
| 20' | 7.429 | 7.445 | 7.462 | 7.478 | 7.495 | 7.511 | 7.528 | 7.545 | 7.562 | 7.579 | 7.596 |
| 30' | 7.596 | 7.613 | 7.63 | 7.647 | 7.665 | 7.682 | 7.7 | 7.717 | 7.735 | 7.753 | 7.77 |
| 40' | 7.77 | 7.788 | 7.806 | 7.824 | 7.842 | 7.861 | 7.879 | 7.897 | 7.916 | 7.934 | 7.953 |
| 50' | 7.953 | 7.972 | 7.991 | 8.009 | 8.028 | 8.048 | 8.067 | 8.086 | 8.105 | 8.125 | 8.144 |
| 83°00' | 8.144 | 8.164 | 8.184 | 8.204 | 8.223 | 8.243 | 8.264 | 8.284 | 8.304 | 8.324 | 8.345 |
| 10' | 8.345 | 8.366 | 8.386 | 8.407 | 8.428 | 8.449 | 8.47 | 8.491 | 8.513 | 8.534 | 8.556 |
| 20' | 8.556 | 8.577 | 8.599 | 8.621 | 8.643 | 8.665 | 8.687 | 8.709 | 8.732 | 8.754 | 8.777 |
| 30' | 8.777 | 8.8 | 8.823 | 8.846 | 8.869 | 8.892 | 8.915 | 8.939 | 8.962 | 8.986 | 9.01 |
| 40' | 9.01 | 9.034 | 9.058 | 9.082 | 9.106 | 9.131 | 9.156 | 9.18 | 9.205 | 9.23 | 9.255 |
| 50' | 9.255 | 9.281 | 9.306 | 9.332 | 9.357 | 9.383 | 9.409 | 9.435 | 9.461 | 9.488 | 9.514 |
| 84°00' | 9.514 | 9.541 | 9.568 | 9.595 | 9.622 | 9.649 | 9.677 | 9.704 | 9.732 | 9.76 | 9.788 |
| 10' | 9.788 | 9.816 | 9.845 | 9.873 | 9.902 | 9.931 | 9.96 | 9.989 | 10.02 | 10.05 | 10.08 |
| 20' | 10.08 | 10.11 | 10.14 | 10.17 | 10.2 | 10.23 | 10.26 | 10.29 | 10.32 | 10.35 | 10.39 |
| 30' | 10.39 | 10.42 | 10.45 | 10.48 | 10.51 | 10.55 | 10.58 | 10.61 | 10.64 | 10.68 | 10.71 |
| 40' | 10.71 | 10.75 | 10.78 | 10.81 | 10.85 | 10.88 | 10.92 | 10.95 | 10.99 | 11.02 | 11.06 |
| 50' | 11.06 | 11.1 | 11.13 | 11.17 | 11.2 | 11.24 | 11.28 | 11.32 | 11.35 | 11.39 | 11.43 |
| 85°00' | 11.43 | 11.47 | 11.51 | 11.55 | 11.59 | 11.62 | 11.66 | 11.7 | 11.74 | 11.79 | 11.83 |
| 10' | 11.83 | 11.87 | 11.91 | 11.95 | 11.99 | 12.03 | 12.08 | 12.12 | 12.16 | 12.21 | 12.25 |
| 20' | 12.25 | 12.29 | 12.34 | 12.38 | 12.43 | 12.47 | 12.52 | 12.57 | 12.61 | 12.66 | 12.71 |
| 30' | 12.71 | 12.75 | 12.8 | 12.85 | 12.9 | 12.95 | 13 | 13.05 | 13.1 | 13.15 | 13.2 |
| 40' | 13.2 | 13.25 | 13.3 | 13.35 | 13.4 | 13.46 | 13.51 | 13.56 | 13.62 | 13.67 | 13.73 |
| 50' | 13.73 | 13.78 | 13.84 | 13.89 | 13.95 | 14.01 | 14.07 | 14.12 | 14.18 | 14.24 | 14.3 |
| 86°00' | 14.3 | 14.36 | 14.42 | 14.48 | 14.54 | 14.61 | 14.67 | 14.73 | 14.8 | 14.86 | 14.92 |
| 10' | 14.92 | 14.99 | 15.06 | 15.12 | 15.19 | 15.26 | 15.33 | 15.39 | 15.46 | 15.53 | 15.6 |
| 20' | 15.6 | 15.68 | 15.75 | 15.82 | 15.89 | 15.97 | 16.04 | 16.12 | 16.2 | 16.27 | 16.35 |
| 30' | 16.35 | 16.43 | 16.51 | 16.59 | 16.67 | 16.75 | 16.83 | 16.92 | 17 | 17.08 | 17.17 |
| 40' | 17.17 | 17.26 | 17.34 | 17.43 | 17.52 | 17.61 | 17.7 | 17.79 | 17.89 | 17.98 | 18.07 |
| 50' | 18.07 | 18.17 | 18.27 | 18.37 | 18.46 | 18.56 | 18.67 | 18.77 | 18.87 | 18.98 | 19.08 |
| 87°00' | 19.08 | 19.19 | 19.3 | 19.41 | 19.52 | 19.63 | 19.74 | 19.85 | 19.97 | 20.09 | 20.21 |
| 10' | 20.21 | 20.33 | 20.45 | 20.57 | 20.69 | 20.82 | 20.95 | 21.07 | 21.2 | 21.34 | 21.47 |
| 20' | 21.47 | 21.61 | 21.74 | 21.88 | 22.02 | 22.16 | 22.31 | 22.45 | 22.6 | 22.75 | 22.9 |
| 30' | 22.9 | 23.06 | 23.21 | 23.37 | 23.53 | 23.69 | 23.86 | 24.03 | 24.2 | 24.37 | 24.54 |
| 40' | 24.54 | 24.72 | 24.9 | 25.08 | 25.26 | 25.45 | 25.64 | 25.83 | 26.03 | 26.23 | 26.43 |
| 50' | 26.43 | 26.64 | 26.84 | 27.06 | 27.27 | 27.49 | 27.71 | 27.94 | 28.17 | 28.4 | 28.64 |
| 88°00' | 28.64 | 28.88 | 29.12 | 29.37 | 29.62 | 29.88 | 30.14 | 30.41 | 30.68 | 30.96 | 31.24 |
| 10' | 31.24 | 31.53 | 31.82 | 32.12 | 32.42 | 32.73 | 33.05 | 33.37 | 33.69 | 34.03 | 34.37 |
| 20' | 34.37 | 34.72 | 35.07 | 35.43 | 35.8 | 36.18 | 36.56 | 36.96 | 37.36 | 37.77 | 38.19 |
| 30' | 38.19 | 38.62 | 39.06 | 39.51 | 39.97 | 40.44 | 40.92 | 41.41 | 41.92 | 42.43 | 42.96 |
| 40' | 42.96 | 43.51 | 44.07 | 44.64 | 45.23 | 45.83 | 46.45 | 47.09 | 47.74 | 48.41 | 49.1 |
| 50' | 49.1 | 49.82 | 50.55 | 51.3 | 52.08 | 52.88 | 53.71 | 54.56 | 55.44 | 56.35 | 57.29 |
| 89°00' | 57.29 | 58.26 | 59.27 | 60.31 | 61.38 | 62.5 | 63.66 | 64.86 | 66.11 | 67.4 | 68.75 |
| 10' | 68.75 | 70.15 | 71.62 | 73.14 | 74.73 | 76.39 | 78.13 | 79.94 | 81.85 | 83.84 | 85.94 |
| 20' | 85.94 | 88.14 | 90.46 | 92.91 | 95.49 | 98.22 | 101.1 | 104.2 | 107.4 | 110.9 | 114.6 |
| 30' | 114.6 | 118.5 | 122.8 | 127.3 | 132.2 | 137.5 | 143.2 | 149.5 | 156.3 | 163.7 | 171.9 |
| 40' | 171.9 | 180.9 | 191 | 202.2 | 214.9 | 229.2 | 245.6 | 264.4 | 286.5 | 312.5 | 343.8 |
| 50' | 343.8 | 382 | 429.7 | 491.1 | 573 | 687.5 | 859.4 | 1146 | 1719 | 3438 |