Таблица Брадиса или тригонометрическая таблица углов представляет собой значение углов в градусном и радиальном измерении. Автор этих математических таблиц – советский педагог, преподававший математику в Твери, Владимир Модестович Брадис, который в своих таблицах рассчитал и свел с точностью до четырёх знаков логарифмы и значения тригонометрических значений в натуральном и градусном исчислении.
Эти таблицы названы «Четырёхзначные математические таблицы» и название сохранено до сегодняшнего дня, хотя впервые они увидели свет в 1921 году. В таблицах даются значение тригонометрических функций в числах и, соответственно, в градусах. Прошло почти сто лет и многие могут спросить – зачем нужна таблица Брадиса и для чего её сейчас можно использовать. Но рассмотрим все по порядку.
Если раскрыть правила ЕГЕ на 2019 год, можно увидеть, что пользоваться калькулятором при сдаче ЕГЕ по математике запрещено, независимо от того, какие функции присутствуют или отсутствуют в этом устройстве. Вместе с тем, указано, что при решении задач, которые содержатся в экзаменационном листе, выдаются необходимые справочные материалы. Это могут быть и четырехзначные таблицы Брадиса, если в этом будет необходимость, которыми экзаменующийся должен уметь пользоваться. Это и поиск угла по таблице тригонометрических значений, и решение с помощью этих данных задач по тригонометрии. Давайте рассмотрим, как пользоваться таблицей Брадиса.
Как таблицы Брадиса работают в реальном решении задач
Так как при решении задач на ЕГЕ пользовать ни обычным калькулятором, ни тем более он-лайн запрещено, можно научиться пользоваться таблицами самому, это, кстати, совсем просто.
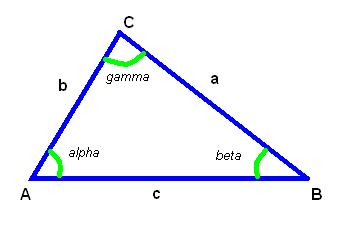
Можно находить углы треугольника по имеющимся сторонам, а можно найти сторону треугольника, имея в выходных данных угол и сторону треугольника. Для этого используем теорему синусов.
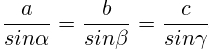
Отсюда:
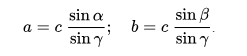
Аналогично находим сторону с.
Или теорему косинусов:
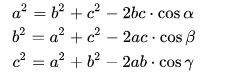
Знаем также, что сумма всех углов должна быть равна 180 градусов.
По формуле пропорциональности находим искомую величину. Если мы искали угол, при помощи таблицы переводим численное значение его в градусы, если мы будем искать сторону, угол, который получили в исходных данных в градусах, переводим с помощью таблицы в числовое значение. Основное замечание: если задача стоит на поиск угла, разумнее применять теорему косинусов, так как синус при расчете в вершине треугольника может получится как 30 градусов, так и 150, если в задании не оговаривается то, что угол не может быть тупым. Поэтому теорема косинусов в таком случае предпочтительнее.
Например, мы имеем три длины сторон треугольника, нужно найти три угла. Основным решением задачи будет условие, что каждая из сторон треугольника по длине не может быть равной или больше. Допустим, есть сторона а= 5; с=12; b= 10;
![]()
условие выполняется.
Что бы найти угол ![]() , применяем формулу:
, применяем формулу:
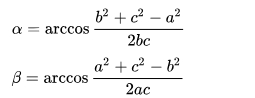
α= arccos (25+ 144 – 100): 2х120; α= arccos 0,2875; В таблице косинусов на пересечении со стороны косинусов находим значение, 0,2874, близкое к нашему полученному в результате вычислений. Это угол α 74°42′. Аналогично рассчитываем угол β.
Затем, согласно правилам суммы трёх углов, находим третий угол:
![]()
По такой же схеме находим угол и две стороны, если заданы сторона и два угла, прямоугольные треугольники решаются по теореме Пифагора, когда один из углов известный и он равен 90 градусов плюс необходимо иметь в данных задачи ещё два элемента. Это могут быть два катета, катет и гипотенуза, катет и прилежащий к нему острый угол, катет и противолежащий острый угол, гипотенуза и один из острых углов. Берем пример, когда мы имеем прямоугольный треугольник
Используем одну из формул:
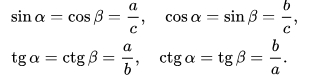
Также применяем формулу:

Как практически пользоваться таблицей Брадиса
В таблице синусов и косинусов есть значения углов от 0 градусов до 90 градусов. Если у нас в результате вычислений получилось число, например, SIN 0,7254. Находим на пересечении sin/cos 46 градусов, далее по верхней строчке напротив числа находим количество минут. В нашем случае это 30 °. Таким образом угол будет равен 46 градусов и 30 минут.
Если, наоборот, у нас есть угол 22° и 10′, нам нужно найти его значение в радианах. В таблице находим значение только 22 ° и 12 м ′, самое близкое к искомому. Это число 0,3778. Если от 12 минут отнять 10, получим поправку в 2 минуты. Справа в таблице Брадиса находим нашу поправку напротив 22 градусов. Она равна 0, 0005. Так как у нас значение в таблице было больше, чем мы искали, эту поправку нужно отнять: 0, 3778-0,0005=0, 3773. Это число и вставляем затем в формулу. Аналогично ищем значение косинуса.
Например, нам нужно найти косинус 50 ° 31′. Ищем в таблице тригонометрических значений ближайшее значение (если нет точного значения) – это будет число 0,6361. Поправка на одну минуту даст нам 0, 0002. В случае косинусов поправка имеет отрицательное значение, то есть косинус 50°, 31 ′будет равна cos 50 °, 30 ′+ 1 ′, что в числовом значении будет 0,6361+(-0,0002) = 0, 6359. Таким же образом переводим число в градусы по таблице градусов.
Если нам нужно перевести тангенс или котангенс с радианов в градусы или наоборот, наши действия будут аналогичные, четырехзначная таблица Брадиса всегда поможет в вычислении.
Применение четырехзначной таблицы Брадиса в повседневной жизни
Зачем ещё нужна таблица Брадиса – она может применяться и в наше время в, так называемых, бытовых целях. Это может быть строительство небольшого сооружения, когда нужно уточнить высоту или ширину, подняться по лестнице нет возможности, а все остальное возможно измерить. Если интернет в наличии, можно найти и рассчитать все там, но, к сожалению, часто такой возможности нет, поэтому таблицы, формулы и простой калькулятор помогут высчитать и угол наклона козырька, и высоту стенки или столбика.

Можно смоделировать и самому рассчитать каркас дома, изготовив его в масштабе, таблицы пригодятся во многих вопросах. Если логарифмы используются очень в редких случаях, то с ними можно рассчитать и площадь круга и длину окружности, что иным умельцам очень может пригодиться.