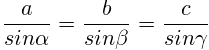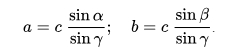Содержание статьи
- Таблица синусов и её применение
- Онлайн калькулятор расчета синуса угла
- Как рассчитать синус угла. Считаем синус 60°, синус 45°, синус 30°
- Что такое таблица синусов π и таблица Брадиса
- Как пользоваться таблицей Брадиса для синусов
Таблица синусов и её применение
Для начала нужно напомнить, что означает такое понятие, как синус угла.
Синус – это отношение катета, находящегося напротив этого угла к гипотенузе. В нашей статье показано, как научиться находить значение синуса (sin) углов, от 0 до 90° и применять это при решении задач.
Это справедливо в случае, если треугольник прямоугольный.
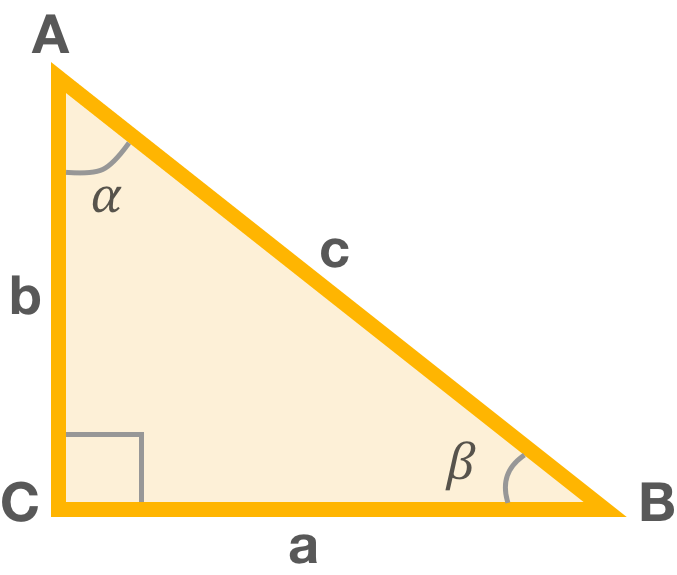
Пример: найдем синус угла ⍺ и угла β
sin ⍺ = а/с или отношение стороны ВС к стороне АВ. Если брать угол β, то противостоящим будет считаться сторона b или АС. Гипотенуза в данном случае та же – AB. Тогда:
sin β = b/с или АС отношение АВ.
В прямоугольном треугольнике всегда 2 катета и только одна гипотенуза
Как известно, целых значений угла – 360. Но часто нужно рассчитать значения для самых популярных углов, таких как: синус 0°, синус 30°, синус 45°, синус 60°, синус 90°. Эти значения можно найти в таблицах Брадиса и без расчётов.
Если взять тригонометрическую таблицу Брадиса для решения задач, можно убедиться на личном примере, что таблица синусов является одной из наиболее применяемых таблиц. Эта статья посвящена тому, как научиться находить значение синуса (sin) углов, от 0 до 90° и научиться это значение применять для решения задач. Кстати, её разработал и опубликовал в 1921 году педагог из Твери Владимир Модестович БРАДИС
Несмотря на то, что в 2021 году она отметит свой столетний юбилей, актуальность таблица Брадиса не утратила. В частности ее применяют архитекторы, проектанты, конструктора для проведения быстрых промежуточных расчетов.
Таблицы Брадиса разрешены к использованию в школах при сдаче ЕГЭ, в отличие от калькуляторов.
Онлайн калькулятор расчета синуса угла
Как рассчитать синус угла.Считаем синус 60°,синус 45°, синус 30°
Некоторые значения синуса угла можно рассчитать достаточно просто, воспользовавшись таблицей синусов угла π (пи) в радианах.
π (пи) равно 3,14 или 180°
Пример: рассчитаем значения синуса следующих углов: 0°, 30°, 45°, 60°, 90° в радианах с использованием π (пи)
Берем синус 0°, в радианах он будет 0, тут даже считать нечего.
Синус 30° равен π/6.
Потому что “все” π (пи) – это половина окружности или 180°. Поэтому 30° – это все 180° разделенные на 6. По таком же принципу находим значения синусов для остальных углов.
Синус 45° равен π/4 (180 градусов разделенные на 4).
Синус 60° равен π/3 (180 градусов разделенные на 3).
Синус 90° равен π/2 или 1 (180 градусов разделенные на 2).
Остальное дело калькулятора – просто переводим π в 3,14 и делим на нужное число 6, 4, 3 или 2.
Но часто нужно решить задачу для каких то либо целей практических, при котором значения углов будут другими, не такими популярными, а теми, которые получились в виде вычислений или измерений. Далее следует пример решения такой задачи.
Пример: рассмотрим прямоугольный треугольник, в котором катеты а и b имеют значение 5 и 2√6, нужно найти синус каждого острого угла. Рисунок и обозначения стандартные (смотри выше).
Используя теорему Пифагора, которая гласит, что “квадрат гипотенузы равен сумме квадратов двух катетов“, находим гипотенузу:
С₂=5х5+ (2√6)х(2√6) = 25 + 4х6 = 49 (см). Итог: С₂ = 7 (см).
Нам известно, что синус это есть отношение катета, который противолежит к искомому углу, к гипотенузе. То есть sin α = a/c, это значит, что sin α =5/7. Соответственно, sin β= b/с ,и sin β равен 2√6/7.
Теперь пробуем найти точное значение синуса и через таблицы Брадиса, найдя число 5/7, затем по таблице найти соответствующее ему значение угла в градусах. Потом от 90° отнимаем это значение, получаем градусы и переводим его в радианы.
Можно использовать формулу из теоремы синусов.
Её можно использовать в случае, если у нас известна гипотенуза треугольника и два угла или один из катетов. Тогда в соответствии с правилами пропорции находим:
Что найти синус угла, к примеру: α = 42°, угол β =48 °, открываем таблицу Брадиса. Так как у нас углы без минут, находим значение синуса угла по первой колонке. Sin α = 0,6691, sin β = 0,7431. Пусть в условии сторона с = 9 см, Синус 90° = 1. Подставляем значение и получаем: а = 9 х (0,6691: 1) = 6, 0219 (см).
Что такое таблица синусов π и таблица Брадиса
В таблице синусов значение угла α дается в:
-
- радианах,
-
- градусах,
- в виде числа, выраженного через квадратный корень.
Это таблица не только для синусов, но и для других тригонометрических знаков. Но в данном случае, мы приведем таблицу только для синусов.
| Значение угла α (градусов) | Значение угла α в радианах (через число пи) | sin (синус) |
|---|---|---|
| 0 | 0 | 0 |
| 15 | π/12 | (√3 - 1)/2√2 |
| 30 | π/6 | 1/2 |
| 45 | π/4 | √2/2 |
| 60 | π/3 | √3/2 |
| 75 | 5π/12 | (√3 + 1)/2√2 |
| 90 | π/2 | 1 |
| 105 | 7π/12 | (√3 + 1)/2√2 |
| 120 | 2π/3 | √3/2 |
| 135 | 3π/4 | √2/2 |
| 150 | 5π/6 | 1/2 |
| 180 | π | 0 |
| 210 | 7π/6 | -1/2 |
| 240 | 4π/3 | -√3/2 |
| 270 | 3π/2 | -1 |
| 360 | 2π | 0 |
Рассчитываем калькулятором значение π, данные можно посмотреть в таблице. Здесь включены значения синуса, которых нет в таблицах Брадиса, вычисления сделаны с точностью до 4 знака. Если нужно узнать, чему равен синус, это всегда можно посмотреть в таблице или рассчитать самому.
| Значение sin угла α в градусах | Значение sin угла α в радианах | Значение синуса угла α |
|---|---|---|
| Синус угла 0 градусов | 0 | 0 |
| Синус угла 15 градусов | π/12 | 0.2588 |
| Синус угла 30 градусов | π/6 | 0.5 |
| Синус угла 45 градусов | π/4 | 0.7071 |
| Синус угла 50 градусов | 5π/18 | 0.766 |
| Синус угла 60 градусов | π/3 | 0.866 |
| Синус угла 65 градусов | 13π/36 | 0.9063 |
| Синус угла 70 градусов | 7π/18 | 0.9397 |
| Синус угла 75 градусов | 5π/12 | 0.9659 |
| Синус угла 90 градусов | π/2 | 1 |
| Синус угла 105 градусов | 5π/12 | 0.9659 |
| Синус угла 120 градусов | 2π/3 | 0.866 |
| Синус угла 135 градусов | 3π/4 | 0.7071 |
| Синус угла 140 градусов | 7π/9 | 0.6428 |
| Синус угла 150 градусов | 5π/6 | 0.5 |
| Синус угла 180 градусов | π | 0 |
| Синус угла 270 градусов | 3π/2 | -1 |
| Синус угла 360 градусов | 2π | 0 |
Как пользоваться таблицей Брадиса для синусов
Научиться находить синус угла практически по таблице Брадиса можно на таком примере:
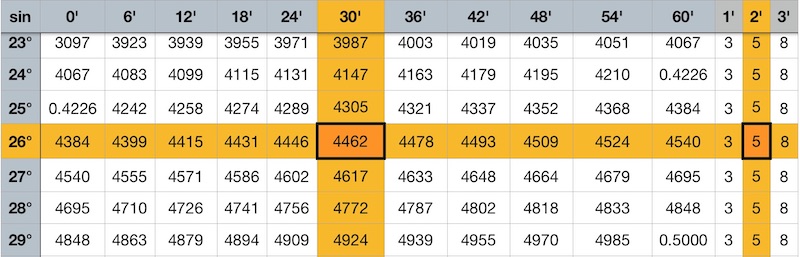
Пример: требуется найти числовое значение угла 26°32′
Для того, что бы найти числовое значение, находим в таблице значение, которое наиболее близкое, это синус 26°30′. Это 0, 4462. Не хватает 2′. Ищем слева напротив значения 2′ – это будет 0,0005. Прибавляем это число к полученному : 0,4462+0,0005= 0,4467. Всё просто!
| sin | 0' | 6' | 12' | 18' | 24' | 30' | 36' | 42' | 48' | 54' | 60' | 1' | 2' | 3' |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sin | 60' | 54' | 48' | 42' | 36' | 30' | 24' | 18' | 12' | 6' | 0' | 1' | 2' | 3' |
| 0.0000 | ||||||||||||||
| 0° | 0.0000 | 17 | 35 | 52 | 70 | 87 | 105 | 122 | 140 | 157 | 175 | 3 | 6 | 9 |
| 1° | 175 | 192 | 209 | 227 | 244 | 262 | 279 | 297 | 314 | 332 | 349 | 3 | 6 | 9 |
| 2° | 349 | 366 | 384 | 401 | 419 | 436 | 454 | 471 | 488 | 506 | 523 | 3 | 6 | 9 |
| 3° | 523 | 541 | 558 | 576 | 593 | 610 | 628 | 645 | 663 | 680 | 698 | 3 | 6 | 9 |
| 4° | 698 | 715 | 732 | 750 | 767 | 785 | 802 | 819 | 837 | 854 | 0.0872 | 3 | 6 | 9 |
| 5° | 0.0872 | 889 | 906 | 924 | 941 | 958 | 976 | 993 | 1011 | 1028 | 1045 | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 0.1736 | 3 | 6 | 9 |
| 10° | 0.1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 3 | 6 | 9 |
| 13° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 0.2588 | 3 | 6 | 8 |
| 15° | 0.2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 3 | 6 | 8 |
| 16° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 3 | 6 | 8 |
| 17° | 2942 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 3 | 6 | 8 |
| 18° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 0.3420 | 3 | 5 | 8 |
| 20° | 0.3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 3 | 5 | 8 |
| 21° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 3 | 5 | 8 |
| 23° | 3097 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 0.4226 | 3 | 5 | 8 |
| 25° | 0.4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 3 | 5 | 8 |
| 27° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 3 | 5 | 8 |
| 28° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 0.5000 | 3 | 5 | 8 |
| 30° | 0.5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 3 | 5 | 8 |
| 31° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 0.5736 | 2 | 5 | 7 |
| 35° | 0.5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 0.5878 | 2 | 5 | 7 |
| 36° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 2 | 5 | 7 |
| 38° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 0.6428 | 2 | 4 | 7 |
| 40° | 0.6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 2 | 4 | 6 |
| 43° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 8909 | 6921 | 6934 | 6947 | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 0.7071 | 2 | 4 | 6 |
| 45° | 0.7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 2 | 4 | 6 |
| 46° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 0.7660 | 2 | 4 | 6 |
| 50° | 0.7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 2 | 4 | 5 |
| 52° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 2 | 3 | 5 |
| 54° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 0.8192 | 2 | 3 | 5 |
| 55° | 0.8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 2 | 3 | 5 |
| 56° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 2 | 3 | 5 |
| 58° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 0.8660 | 1 | 3 | 4 |
| 60° | 0.8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 1 | 3 | 4 |
| 61° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 1 | 3 | 4 |
| 63° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 0.9063 | 1 | 3 | 4 |
| 65° | 0.9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9256 | 9272 | 1 | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9383 | 9391 | 0.9397 | 1 | 2 | 3 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 0.9455 | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 0.9659 | 1 | 2 | 2 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 1 | 1 | 2 |
| 76° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 1 | 1 | 2 |
| 79° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 0.9848 | 1 | 1 | 2 |
| 80° | 0.9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 0 | 1 | 1 |
| 81° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 0 | 1 | 1 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0.9998 | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0 | 0 | 0 |
| 90° | 1.0000 |